Préparation TP analyse de données¶
Marc BUFFAT, dpt mécanique, Université Lyon 1

[1] librement inspiré par le cours "Engineering Computations" du Pr L. Barba (Washington Univ.)
Objectifs du TP¶
Apprendre à lire des données dans un fichier, les analyser et les traiter pour en déduire des prédictions. Le cas étudié concerne le problème du réchauffement climatique.
- lecture des données
- analyse des données
- lissage des données avec une droite (la droite des moindres carrées) pour obtenir un modèle
- prédiction en utilisant le modèle
- analyse des résultats
Evolution de la Température de la Terre¶
Dans cette leçon, nous appliquerons tout ce que nous avons appris (et plus) pour analyser des données d'évolution de la température de la Terre au cours du temps.
Les questions adressées, qui sont brûlante dans le monde d'aujourd'hui, sont:
- La température de la terre augmente-t-elle?
- Et de combien?
Les données sur l'évolution de la température terrestre sont disponibles à partir de plusieurs sources: la NASA, le National Climatic Data Center (NCDC) et l'Université d'East Anglia au Royaume-Uni. Consultez le site de University Corporation for Atmospheric Research (UCAR) pour une discussion approfondie.
Le NASA Goddard Space Flight Center est l'une des sources de données climatiques mondiales. Ils ont produit la vidéo ci-dessous montrant une carte en couleur de l'évolution de la surface globale anomalies de température de 1880 à 2015.
Le terme anomalie de température globale désigne la différence de température par rapport à une valeur de référence ou à une moyenne à long terme. C'est une manière très utile de regarder le problème et à bien des égards meilleur que la température absolue.
Regarder la video suivante sur l'évolution de la température moyenne de la terre
# video sur l'evolution de la température
from IPython.display import YouTubeVideo
YouTubeVideo('gGOzHVUQCw0')
Méthode d'analyse¶
Comment pourrions-nous comprendre les tendances à partir des données sur la température mondiale?
La première étape de l'analyse de données consiste à générer des graphiques simples en utilisant Matplotlib. Nous allons regarder l'historique des anomalies de température, contenu dans un fichier, et faire notre premier tracé pour explorer ces données.
Nous allons lisser les données, puis nous les ajusterons avec une droite pour trouver une tendance.
Étape 1: lire les données¶
Les données sont issues de la page Web NOAA (National Oceanic and Atmospheric Administration). Nous avons utilisé des données entre 1880 et aujourd'hui, mais vous pouvez utiliser des données actualisées à partir de ce même site.
Dans le répertoire data, nous avons un fichier nommé anomalie_temperature.csv. Ce fichier contient l'année sur la première colonne, et les moyennes des anomalies de température du sol répertoriées séquentiellement sur la deuxième colonne, à partir de 1880 jusqu'à nos jours. Nous allons charger le fichier, puis faire un premier tracé pour voir à quoi il ressemble.
En utilisant la commande unix/linux head mon_fichier, on affiche les 10 premières lignes du fichier mon_fichier
Attention vous n'avez pas tous les mêmes données, donc ne vous contentez pas de comparer les résultats bruts, mais essayer de comprendre la méthode.
lecture du fichier¶
Pour charger les données à partir du fichier, nous utiliserons la fonction numpy.loadtxt(), qui nous permet de sauvegarder directement les données lues dans des tableaux NumPy. (
Les données sont séparées par des , et on veut enregistrer directement les données dans les deux tableaux annee et anomalie_temp. On va donc fournir des arguments à la fonction np.loadtxt pour l'utiliser (voir la documentation de loadtxt)
annee, anomalie_temp = np.loadtxt(fichier, delimiter=',', unpack=True)
On utilisera donc cette fonction pour lire les données dans les deux tableaux annee et anomalie_temp.
C'est pour pouvoir utiliser cette fonction que l'on a importer la bibliothéque numpy
import numpy as np
tracer des données¶
Nous utiliserons la librairie matplotlib pour tracer la courbe d'évolution des anomalies de température en fonction de l'année.
Cette courbe est très bruitée, on va donc la lisser pour pouvoir en déduire un modèle.
Etape 2: régression linéaire par moindres carrés¶
Afin d'avoir une idée du comportement général de ces données, nous allons chercher une courbe qui correspond (approximativement) aux points de mesure. Nous recherchons une courbe simple (par exemple, un polynôme de degré 1) qui permet de lisser le bruit toujours présent dans les données expérimentales.
Soit $f (x)$ la fonction que nous ajusterons aux $n+1$ points expérimentaux: $ (x_i, y_i) $, $ i = 0, 1, ..., n $:
La fonction dépend de 2 paramêtres $a_0,a_1$ $$ f (x) = a_0 + a_1 x $$
Il reste alors à déterminer les 2 paramètres $a_0$ et $a_1$ qui donneront la "meilleure approximation" par rapport aux données, c.a.d qui minimiseront l'écart $Err$ entre la courbe et les points de mesure.
Cet écart $Err$ est mesuré avec une norme: la norme des moindres carrés
$$ Err = \sum_{i=0}^N (f(x_i) - y_i)^2 = \sum_{i=0}^N (a_0 + a_1 x_i - y_i)^2 $$On montre que cette erreur erreur est minimale si l'on choisit $a_1$ et $a_0$ tels que
\begin{eqnarray} a_1 = \frac{\sum_{i = 0}^{n} y_ {i} (x_i - \bar{x})} {\sum_{i = 0}^{n} x_i (x_i - \bar{x })} \quad, \quad a_0 = \bar {y} - a_1 \bar {x} \end{eqnarray}où $\bar {x}$ est la moyenne des ${x_i}$ et $\bar {y}$ la moyenne des ${y_i}$
Le graphique ci-dessous montre un exemple de lissage de données par la droite des moindres carrées
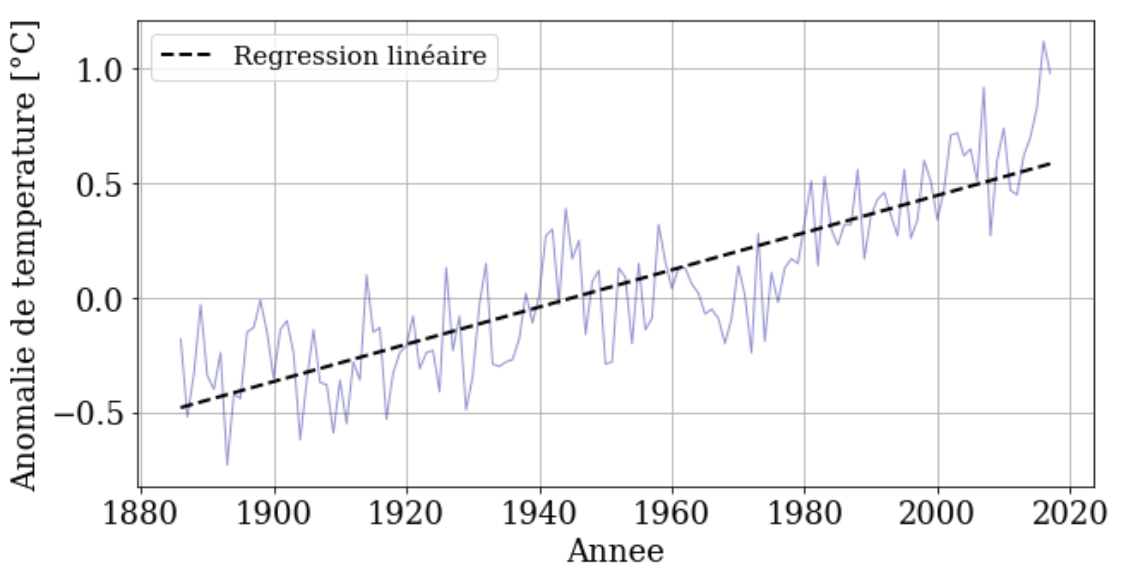
Dans la cellule suivante, vous trouverez les éléments de théories justifiant ce calcul.
Un peu de thèorie¶
Lorsque les oordonnées $y$ des points de données sont bruitées, il est courant d'utiliser un lissage par moindres carrés, qui consiste à minimiser l'erreur quadratique $Err$ entre la fonction $f$ et les points de mesure. Dans notre cas on cherche une fonction $f(x) = a_0 + a_1 x$ à 2 paramètres $a_0$ et $a_1$
\begin{equation} Err(a_0, a_1) = \sum_{i = 0}^ {n} [y_i - f (x_i)] ^ 2 \end{equation}La condition de minimisation de cette fonctions de 2 variables $Err(a_0, a_1)$ est que la dérivée par rapport à chacune des variables s'annulle, ce qui dans notre cas conduit aux 2 équations:
\begin{equation} \frac{\partial{Err}} {\partial{a_0}} = 0,\;\;\; \frac{\partial{Err}} {\partial{a_1}} = 0,\label{eq1} \end{equation}qui traduisent la condition de minimisation $\vec{\nabla} Err = \vec{0}$
Régression linéaire¶
La fonction de lissage la plus simple est la régression linéaire, qui ajuste une ligne droite aux données. Dans ce cas,
\begin{equation} f (x) = a_0 + a_1x \end{equation}La fonction à minimiser s'écrit:
\begin{equation} Err(a_0, a_1) = \sum_{i = 0}^{n} [y_i - f (x_i)]^2 =\sum_{i = 0}^ {n} (y_i - a_0 - a_1x_i)^2 \end{equation}Les équations de minimisation de $Err$ deviennent:
\begin{equation} \frac{\partial{Err}}{\partial{a_0}} = \sum_{i = 0}^ {n} -2 (y_i - a_0 - a_1x_i) = 2 \left[a_0 (n + 1) + a_1 \sum_{i = 0}^{n} x_i -\sum_ {i = 0}^{n} y_i \right] = 0 \label{eq2} \end{equation}et
\begin{equation} \frac{\partial{Err}}{\partial{a_1}} = \sum_{i = 0}^{n} -2 (y_i - a_0 - a_1x_i) x_i = 2 \left[a_0 \sum_{i = 0 }^{n} x_i + a_1 \sum_{i = 0}^{n} x_ {i}^ 2 - \sum_{i = 0}^{n} x_iy_i \right] = 0 \label{eq3} \end{equation}Divisons les deux équations par $ 2 (n + 1) $ et réorganisons les termes.
Réorganisation $\eqref{eq2}$:
\begin{eqnarray} 2 \left[a_0 (n + 1) + a_1 \sum_{i = 0}^{n} x_i - \sum_{i = 0}^{n} y_i \right] & = 0 \nonumber \\ a_0 \frac{(n + 1)} {n + 1} + a_1 \frac {\sum_{i = 0}^{n} x_i} {n + 1} - \frac{\sum_{i = 0}^{n} y_i} {n + 1} & = 0 \\ \end{eqnarray}soit $$ a_0 = \bar {y} - a_1 \bar {x} \label{eq4} $$
où $\bar{x} = \frac{\sum_{i = 0}^{n} x_i}{n + 1}$ et $\bar{y} = \frac{\sum_{i = 0}^{ n} y_i} {n + 1}$ sont respectivement la moyenne des $\left( x_i \right)$ et des $\left( y_i \right)$
Réorganisation maintenant $\eqref{eq3}$:
\begin{eqnarray} 2 \left[a_0 \sum_{i = 0}^{n} x_i + a_1 \sum_{i = 0}^{n} x_ {i}^ 2 - \sum_{i = 0}^{n} x_iy_i \right] & = 0 \\ a_0 \sum_{i = 0}^{n} x_i + a_1 \sum_{i = 0}^ {n} x_ {i}^ 2 - \sum_{i = 0}^{n} x_iy_i & = 0 \label{eq5}\\ \end{eqnarray}Maintenant, si nous remplaçons $a_0$ de l'équation $\eqref{eq4}$ dans $\eqref{eq5}$ et réorganisons les termes:
\begin{eqnarray*} (\bar{y} - a_1 \bar{x}) \sum_{i = 0}^{n} x_i + a_1 \sum_{i = 0}^ {n} x_{i}^2 - \sum_{i = 0}^{n} x_iy_i & = 0 \\ \end{eqnarray*}En remplaçant les définitions des valeurs moyennes dans l'équation,
\begin{eqnarray*} \left[\frac{1}{n + 1} \sum_{i = 0}^{n} y_i - \frac{a_1}{n + 1}\sum_{i = 0}^{n} x_i \right] \sum_{i = 0}^{n} x_i + a_1\sum_{i = 0}^{n}x_ {i}^ 2 - \sum_{i = 0}^{n} x_iy_i & = 0 \\ \frac{1}{n + 1} \sum_{i = 0}^{n} y_i \sum_{i = 0}^{n} x_i -\frac{a_1} {n + 1} \sum_{i = 0}^{n} x_i \sum_{i = 0}^{n} x_i + a_1 \sum_{i = 0}^{n} x_{i} ^ 2 - \sum_{i = 0}^{n} x_iy_i & = 0 \\ \end{eqnarray*}En remplaçant $\frac{\sum_{i = 0}^{n} x_i}{n + 1} = \bar{x}$,
\begin{eqnarray*} \sum_{i = 0}^{n} y_i \bar{x} - a_1 \sum_{i = 0}^{n} x_i \bar{x} + a_1 \sum_{i = 0}^{n} x_{i}^2 - \sum_{i = 0}^{n} x_iy_i = 0 \end{eqnarray*}en mettant les termes en $ a_1 $ à gauche:
\begin{eqnarray*} a_1 \left[\sum_{i = 0}^{n} x_ {i}^ 2 -\sum_{i = 0}^{n} x_i \bar{x} \right] & = \sum_{i = 0 }^{n} x_iy_i -\sum_{i = 0}^{n} y_i \bar{x} \\ a_1 \sum_{i = 0}^{n} (x_ {i}^ 2 - x_i \bar{x}) & = \sum_{i = 0}^ {n} (x_iy_i - y_i \bar{x}) \\ a_1 \sum_{i = 0}^{n} x_ {i} (x_ {i} - \bar{x}) & = \sum_{i = 0}^ {n} y_i (x_i - \bar{x} ) \end{eqnarray*}on obtiens la valeur de $a_1$:
\begin{eqnarray} a_1 = \frac{\sum_{i = 0}^{n} y_{i} (x_i - \bar{x})} {\sum_{i = 0}^{n} x_i (x_i - \bar{x })} \end{eqnarray}D'où l'expression des coefficients $a_1$ et $a_0$ sont:
\begin{eqnarray} a_1 = \frac{\sum_{i = 0}^{n} y_ {i} (x_i - \bar{x})} {\sum_{i = 0}^{n} x_i (x_i - \bar{x })} \quad, \quad a_0 = \bar {y} - a_1 \bar {x} \end{eqnarray}Programmation: calcul des coefficients¶
Pour lisser les données d'anomalie de température pour en déduire l'évolution de la température terrestre, nous utiliserons la régression linéaire par moindres carrés pour calculer la pente $a_1$ et la constante $a_0$
$$ y = a_1 x + a_0 $$avec pour expression des coefficients $a_1$ et $a_0$:
\begin{eqnarray} a_1 = \frac{\sum_{i = 0}^{n} y_ {i} (x_i - \bar{x})} {\sum_{i = 0}^{n} x_i (x_i - \bar{x })} \quad, \quad a_0 = \bar {y} - a_1 \bar {x} \end{eqnarray}En regardant les expressions, on constate que le calcul de $a_1$ et $a_0$ ne fait intervenir que le calcul de la moyenne de tableaux. En effet en notant moyenne(A) une fonction moyenne qui calcule la moyenne $\bar{A}= \frac{1}{n} \sum_{i=0}^{n} A_i$ d'un tableau A de dimension $n$ on peut réécrire les expressions précédentes
sous forme algorithmique
Xm = moyenne(X)
Ym = moyenne(Y)
a1 = moyenne(Y * (X-Xm)) / moyenne (X * (X-Xm))
a0 = Ym - a1*Xm
Dans notre cas, les données X sont dans le tableau annee, et les données Y sont dans le tableau anomalie_temp. Pour calculer nos coefficients avec la formule ci-dessus, nous avons besoin des valeurs moyennes des données. Comme nous devons calculer la moyenne à la fois pour x ety, il est utile d'écrire une fonction Python personnalisée qui calcule la moyenne pour n'importe quel tableau, que l'on peut ensuite réutiliser.
C'est une bonne pratique de programmation d' éviter de répéter les instructions et d'écrire du code qui soit réutilisable, non seulement parce qu'il conduit à moins de temps de développement, mais aussi parce qu'il réduit les erreurs. Si vous devez faire le même calcul plusieurs fois, il vaut mieux l'encapsuler dans une fonction.
Rappelez-vous un des concepts clé de la programmation que l'on a vu ensemble: *Une fonction est une collection compacte de code qui exécute une action sur ses arguments ou données et qui renvoie le résultat.
Une fois défini, vous pouvez appeler une fonction autant de fois que vous le souhaitez. Lorsque nous appelons une fonction, nous exécutons tout le code à l'intérieur de la fonction. Le résultat de l'exécution dépend de la définition de la fonction et des valeurs qui y sont passées en arguments. Les fonctions peuvent ou non renvoyer des valeurs lors de leur dernière opération.
La syntaxe pour définir ses propres fonctions est la suivante:
def nom_fonction (arg_1, arg_2, ...):
'''
docstring: description de la fonction
'''
<corps de la fonction>
return valeur
Le docstring d'une fonction est un message du programmeur documentant ce qu'il a construit. Les docstrings doivent être descriptifs et concis. Ils sont importants car ils expliquent (ou rappellent) l'utilisation prévue de la fonction aux utilisateurs. Vous pouvez accéder ultérieurement à la docstring d'une fonction en utilisant la fonction help () et en passant le nom de la fonction. Si vous êtes dans un notebook, vous pouvez également ajouter un point d'interrogation ? avant le nom de la fonction et exécuter la cellule pour afficher les informations d'une fonction.
Essayez par exemple
print?
ou
help(print)
Pour notre problème vous aurez à définir une fonction moyenne
def moyenne(A):
'''
calcul la moyenne du vecteur A (tableau numpy)
'''
mean = 0
....
return mean
Prédiction¶
Une fois que l'on a lissé les données , on peut alors faire une prédiction d'anomalies de température pour une année an dans le futur:
Préparation¶
Pour préparer le TP, noter les différentes étapes à éffectuer pour faire cette prédiction:
- calculs à faire
- fonctions python à écrire
- analyse à faire
FIN¶