Cours MGC2028L: outils numériques pour la Mécanique

Dpt de mécanique, Université Lyon 1

Documents sur le cours, python, markdown, matplotlib

Consignes à lire attentivement

A la fin de votre session, pensez bien à vous déconnecter (bouton en haut à gauche se déconnecter)

Remplir la cellule suivante

Ecrire votre nom , prénom et votre numéro d'étudiant ci-dessous Le numéro d'étudiant doit etre un entier !!!

NOM = ""
PRENOM=""
NUMERO_ETUDIANT = None
if type(NUMERO_ETUDIANT) is not int :
    print("ERREUR: numéro d'étudiant non spécifié!!!")

Examen de TP

ATTENTION: pendant la durée de l'examen vous devez rester en mode examen

• Répondre uniquement dans les cellules indiquées et ne pas les déplacer!!

• Les 3 parties sont indépendantes et sont chacune notée sur 10.

notebook_name='examen.ipynb'

import numpy as np
from IPython.display import HTML
from validation.validation import info_etudiant, bib_validation
from validation.valide_markdown import test_markdown, test_code, test_algorithme
bib_validation('cours','MGC2028L')
from Circuit2 import *
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if type(NUMERO_ETUDIANT) is not int :
    NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
#
print("Examen pour {} {} {} : {}".format(NOM,PRENOM,NUMERO_ETUDIANT,notebook_name))
#
np.random.seed(NUMERO_ETUDIANT)
circuit = Circuit("circuit.dat")

%matplotlib inline
# bibliothéque
import numpy as np
import matplotlib.pyplot as plt
# police des titres
plt.rc('font', family='serif', size='18')

Partie I sur 10 pts

On souhaite utiliser python pour étudier l'évolution de la fonction $f$ dont les valeurs en $x$ sont données par une somme infinie: $$f(x)=\sum_{n=1}^{\infty}u_n(x)=\sum_{n=1}^{\infty} \frac{1}{1+n^2x^2} $$

Question 1

1.a) Créez la fonction fraction à deux arguments en entrée x et n et qui retourne la valeur de la fraction définissant $u_n(x)$.

1.b) Affichez la valeur de la fonction fraction pour $x=10$ et $n=6$.

#Fonction fraction à créer:
#def 
#    return

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Question 2

On suppose qu'on peut calculer numériquement de façon raisonnable la somme infinie apparaissant dans la définition de $f$ en prenant comme borne supérieure de la somme un nombre très élevé nlim à la place de l'infini:

$$f(x)\approx\sum_{n=1}^{nlim}u_n(x)=\sum_{n=1}^{nlim} \frac{1}{1+n^2x^2} $$

La valeur de nlim est donnée ci-dessous.

nlim = np.random.randint(10,20)*1000
print("nlim={}".format(nlim))

2.a) En utilisant nlim et une boucle for et la fonction fraction précédente, créez la fonction f qui pour un x donné renvoie la valeur de la somme définissant $f(x)$. Pour parcourir les indices on pourra utiliser np.arange.

2.b) Afficher les valeurs de $f$ pour $x=10$ et $x=100$.

#Fonction f à créer:
def f(x):
    global nlim # ligne ajoutée qui précise juste que nlim est une variable 'globale' déjà définie en dehors de la fonction
    
    
    return

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Question 3

On donne deux entiers a et b.

3.a) Créez un tableau numpy array qu'on nommera xtab rempli de valeurs linéairement espacées entre a et b et avec 100 valeurs.

3.b) En utilisant une boucle for avec enumerate, remplir le tableau numpy ftab avec les valeurs de f pour toutes les valeurs de xtab. On initialisera le tableau ftaben utilisant np.zeros.

3.c) Comment peut-on aussi définir un tableau identique ftabBis à partir de f et xtab sans passer par une boucle?

3.d) Mettre en évidence que les tableaux sont identiques en sélectionnant et affichant :

• les valeurs des trois premiers éléments de ftab et ftabBis.

• les valeurs des trois derniers éléments de ftab et ftabBis.

On utilisera obligatoirement la technique d'extraction d'éléments d'un tableau avec le symbole:.

r=np.random.randint(5,8)
a=r*100
b=r*1000
print("a={}".format(a))
print("b={}".format(b))

xtab=None
ftab=None
ftabBis=None

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Question 4

Les maths disent que quand x tend vers l'infini, $f(x)$ tend vers $$g(x)=\frac{\pi^2}{6x^2}$$ On veut vérifier cela par des tracés.

4.a) Superposez la fonction f et la fonction g sur une même figure. On prendra en abscisse les valeurs de xtab.

On mettra la fonction f avec des ronds bleus et la fonction g en rouge continu. On mettra un titre, des axes et la légende.

4.b) Comparez les deux courbes et commentez le résultat.

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Partie II sur 10 pts

On veut tracer la trajectoire d'un objet dont on connaît les positions x et y qui ont été mesurées et stockées dans un fichier. A partir de ces mesures un peu approximatives, on fera une régression quadratique (moindres carrés avec un polynôme de degré 2). Après avoir répondu à toutes les questions, vous devriez obtenir un graphe comme ci-dessous

Question 1

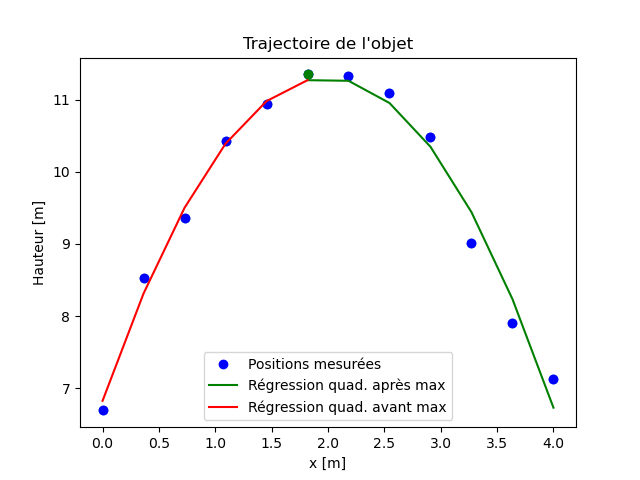
On dispose d'un fichier de données appelé "TrajectoireParabolique.dat" dans lequel la première colonne est l'abscisse x en mètres, la deuxième colonne est l'ordonnée y en mètres. Les données sont séparées par le délimiteur ";".

• Adapter la commande suivante :

  col1, col2 = np.loadtxt("monfichier.dat",delimiter=',',unpack=True)

  pour lire le fichier "TrajectoireParabolique.dat" et mettre dans un tableau numpy appelé x l'abscisse et dans un tableau numpy appelé y l'ordonnée.

x = 0
y = 0
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Question 2

• Tracer les points mesurées de la trajectoire.

On mettra un titre, des axes avec leurs unités.

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Question 3

• Calculer, à l'aide de la fonction np.polyfit, les coefficients $a_2$, $a_1$ et $a_0$ de la régression quadratique, $a_2 x^2 + a_1 x + a_0$. C'est la parabole passant "au plus près" des points de mesure de la trajectoire. Afficher les trois coefficients.
• Tracer la régression quadratique et les mesures sur un même graphique. Mettre un titre, des axes et des légendes.

Indication : a2,a1,a0 = np.polyfit(X,Y,2) régression quadratique des points X,Y avec un polynôme de degré 2

a0 = 0
a1 = 0
a2 = 0

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Question 4

• Écrire la (ou les) instruction(s) pour trouver ymax la valeur du maximum de y.
• Écrire la (ou les) instruction(s) pour trouver xmax la valeur de x où y est maximum.
• Afficher les deux valeurs xmax et ymax

# YOUR CODE HERE
raise NotImplementedError()

Question 5

• A partir de la valeur xmax trouvée dans la question précédente, créer le tableaux numpy xinf qui contient les valeurs de $x\leq $ xmax et le tableaux numpy xsup qui contient les valeurs de $x\geq $ xmax.
• Tracer les points mesurés en bleu, la régression quadratique pour $x\leq $ xmax en rouge, la régression quadratique pour $x\geq $ xmax en vert, le point (xmax,ymax) en vert. Mettre un titre, des axes et des légendes.

Vous devriez obtenir la figure présentée au début de l'exercice.

Indications : pour créer les tableaux xinf et xsup, vous pouvez soit utiliser la fonction np.where vue en cours ou bien des conditions logiques comme vu au TP régression linéaire.

xinf = 0
xsup = 0

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Partie III sur 10 pts

On se propose d'étudier la cinématique d'un point connaissant sa position en fonction du temps.

Pour cela on lit dans le fichier circuit.dat la valeur de 3 tableaux T,X,Y correspondant au temps et à la position X,Y en utilisant la fonction numpy np.loadtxt(). Les valeurs sont en unité SI, i.e. en seconde pour le temps et en mètre pour la position.

Questions 1

dans la cellule suivante:

1. lire la valeur de ces 3 tableaux.
2. calculer la longueur de la trajectoire dans la variable Ltraj.
3. tracer la trajectoire en utilisant la bibliothèque Matplotlib, en particulier les fonctions : plt.xlabel(), plt.ylabel(), plt.title() et la fonction plt.axis('equal') pour avoir des axes avec le même rapport d'aspect.

T = None
X = None
Y = None
Ltraj = 0.
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Question 2

A partir de la position en fonction du temps , on va calculer les composantes de la vitesse en fonction du temps.

Pour cela on calcule la vitesse entre 2 positions successives aux temps $T_i$ et $T_{i+1}$ :

$$ Um_i = \frac{X_{i+1} - X_{i}}{T_{i+1} - T_{i}} \mbox{ et } Vm_i = \frac{Y_{i+1} - Y_{i}}{T_{i+1} - T_{i}}$$

cette vitesse correspond au temps moyen $Tm_i$ entre $T_i$ et $T_{i+1}$ :

$$ Tm_i = \frac{T_{i+1} + T_{i}}{2}$$

Dans la cellule suivante:

1. calculer les temps moyens dans le tableau Tm
2. calculer la vitesse en unité SI à ces instants dans les tableaux Um et Vm

# création des tableaux Tm, Um, Vm
Um, Vm = None, None
Tm = None
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Question 3

1. Calculer le module de la vitesse en km/h dans le tableau Umod.

2. Déterminer la valeur min, max et moyenne du module de la vitesse dans les variables : Umin, Umax et Umean. On affichera ces valeurs.

3. Tracer sur un graphe l'évolution du module en fonction du temps. Sur le graphe, on spécifiera un titre, les labels des axes. Pour mieux analyser le résultat, on pourra utiliser la fonction plt.ylim(ymin,ymax) qui permet de spécifier la limite de l'axe y (pour minimiser l'effet des erreurs d'arrondis).

Umod = None
Umax = Umin = Umean = 0.
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Conclusion

Écrire en quelques lignes l'analyse des résultats dans la cellule suivante en précisant

• la forme de la trajectoire
• le champ de vitesse, sa direction et son module
• que peut-on en déduire sur l'accélération, sa composante normale et tangentielle

Conclusion

YOUR ANSWER HERE

Fin de l'examen

A la fin de l'examen, enregistrer votre travail (bouton à gauche), puis sortir du mode plein écran (esc) et revenir à la fenêtre assignements pour soumettre votre travail !