Cours MGC2028L: outils numériques pour la Mécanique

Dpt de mécanique, Université Lyon 1

Documents sur le cours, python, markdown, matplotlib

Consignes à lire attentivement

A la fin de votre session, pensez bien à vous déconnecter (bouton en haut à gauche se déconnecter)

Remplir la cellule suivante

Ecrire votre nom , prénom et votre numéro d'étudiant ci-dessous Le numéro d'étudiant doit etre un entier !!!

NOM = ""
PRENOM=""
NUMERO_ETUDIANT = None
if type(NUMERO_ETUDIANT) is not int :
    print("ERREUR: numéro d'étudiant non spécifié!!!")

Examen de TP

ATTENTION: pendant la durée de l'examen vous devez rester en mode examen (menu Mode Examen)

• Répondre uniquement dans les cellules indiquées et ne pas les déplacer!!

• Les 3 parties sont indépendantes et sont chacune notée sur 10.

notebook_name='examen.ipynb'

import numpy as np
from IPython.display import HTML
from validation.validation import info_etudiant, bib_validation
from validation.valide_markdown import test_markdown, test_code, test_algorithme
bib_validation('cours','MGC2028L')
from Circuit2 import *
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if type(NUMERO_ETUDIANT) is not int :
    NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
#
print("Examen pour {} {} {} : {}".format(NOM,PRENOM,NUMERO_ETUDIANT,notebook_name))
#
np.random.seed(NUMERO_ETUDIANT)
# valeurs des parametres
_a_ = 9.0 + 0.01*np.random.randint(99)
_N_ = 400 + np.random.randint(100)
_U0_ = 0.5 + 0.01*np.random.randint(100)
_Ttotal_ = 5.

%matplotlib inline
# bibliothéque
import numpy as np
import matplotlib.pyplot as plt
import cv2
# police des titres
plt.rc('font', family='serif', size='18')

Partie I sur 10 pts

On se propose d'étudier le mouvement d'un solide dont les 2 degrés de liberté : un ddl de position (en m) $p(t)$ et un ddl de vitesse (en m/s) $v(t)$ sont solutions du système d'équations différentielles en temps (en s) suivant:

\begin{equation} \dot{\mathbf{Y}} = \mathbf{F}(\mathbf{Y}) \mbox{ avec } \mathbf{Y} = \begin{bmatrix} p(t) \\ v(t) \end{bmatrix} \mbox{ et } \mathbf{F}(\mathbf{Y}) = \begin{bmatrix} v \\ - a\,p \end{bmatrix}. \end{equation}

où $a$ est un paramètre constant strictement positif. On se propose d'étudier le système sur un temps Ttotal en calculant la solution pour N valeurs régulièrement réparties entre 0 et Ttotal. La valeur numérique de ces paramètres est donnée ci-dessous.

Ce système admet une solution analytique simple :

$$ p(t) = \frac{U_0 \sqrt{a}}{a} \sin{(\sqrt{a} \ t)} \;,\; v(t) = U_0 \cos{(\sqrt{a} \ t)} $$

print("paramétres d'étude: a={:.2f} /s-2 , Ttotal={} s , U0 = {:.2f} m/s  N = {}".format(_a_,_Ttotal_,_U0_,_N_))

Paramètres et solution analytique

1. Définir la valeur des paramètres du problème dans les variables a et Ttotal et N
2. Créer un tableau numpy T contenant N valeurs régulièrement réparties entre 0 et Ttotal
3. Dans un tableau numpy Pex, calculer la valeur exacte de la solution p(t) à tous les temps contenus dans T
4. Dans un tableau numpy Vex, calculer la valeur exacte de la solution v(t) à tous les temps contenus dans T
5. En utilisant ces tableaux, tracer la solution analytique p(t) en fonction de t en spécifiant un titre, et des labels pour les axes

# parametres du problème et solution exacte
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

# ne rien écrire dans cette cellule

Fonction smb(Z)

1. Écrire une fonction python smb qui a pour argument un vecteur Z et qui renvoie un vecteur ayant pour valeur $\mathbf{F}(\mathbf{Z})$
2. En utilisant la première valeur des tableaux Pex et Vex, calculer la valeur retournée par cette fonction et la mettre dans la variable dY0 et l'afficher

# second membre 
def smb(Z):
    return
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Calcul de la solution numérique

En utilisant la méthode de Runge Kutta 2 , on va calculer la solution numérique pour ces mêmes temps T.

En partant de la même condition initiale que la solution analytique $Y_0$ à $t=0$ , on calcule la solution $Y_i$ au temps $T_i$ en fonction de la solution $Y_{i-1}$ au temps $T_{i-1}$ et du pas en temps $dt=T_i - T_{i-1}$ par

$$ \begin{align} \mathbf{Y_{m}} & = \mathbf{Y_{i-1}} + \frac{dt}{2} \mathbf{F}(\mathbf{Y_{i-1}}) \\ \mathbf{Y_{i}} & = \mathbf{Y_{i-1}} + dt \,\, \mathbf{F}(\mathbf{Y_{m}}). \end{align} $$

1. Dans un tableau Ynum de N lignes et 2 colonnes, calculer la valeur numérique de la solution
2. En utilisant ce tableau, extraire la solution numérique de p(t) dans le tableau Pnum et la solution numérique de v(t) dans le tableau Vnum. Afficher la première valeur de ces deux tableaux et vérifier qu'elle correspond bien à la solution analytique.
3. En utilisant ces tableaux, tracer la solution numérique de p(t) en fonction de t en spécifiant un titre et des labels pour les axes

# calcul de la solution numérique
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

# ne rien écrire dans cette cellule

Calcul de l'erreur

1. Dans un tableau ErrP, calculer l'écart entre la solution analytique et la solution numérique de p(t)
2. Dans NormEp, calculez la norme euclidienne de l'erreur sur p(t):

$$ \left\lVert {p_{ex} - p_{num}} \right\rVert = \sqrt{\sum_{i=1,N} (p_{ex}(t_i) - p_{num}(t_i))^2} $$

On affichera la valeur de ces variables.

En utilisant ces tableaux, tracer l'évolution de l'erreur sur p(t) en fonction de t en spécifiant un titre, et des labels pour les axes

# calcul de l'erreur
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Analyse

Écrire en markdown dans la cellule suivante votre analyse et vos conclusions sur cette étude, en répondant aux questions:

1. quelle est l'allure de la solution numérique et analytique
2. à quel problème mécanique correspond le système étudié et la condition initiale
3. donner un ordre de grandeur de la précision de la prédiction numérique de la position p(t)
4. donner un commentaire sur la précision de la méthode numérique et son évolution temporelle

Ecrire vos commentaires ici

YOUR ANSWER HERE

Partie II sur 10 pts

Note: Sur cette partie, aucun fichier n'est à lire et charger en mémoire.

Un étudiant souhaite faire le suivi expérimental d'un cylindre de forme elliptique sur un plan incliné. Il a imprimé en 3D ce cylindre en plastique blanc et dessiné au marqueur noir deux points sur une section du cylindre en vue d'étudier leur trajectoire en fonction du temps.

Il utilise une caméra qui prend des images de taille carrée 5120 x 5120 à une fréquence d'acquisition de 41 images/seconde.

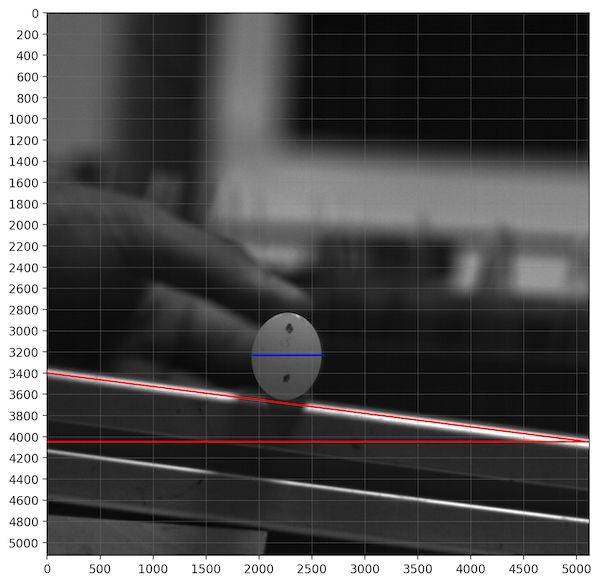
Sur la figure ci-dessus, qui montre une image typique obtenue (en utilisant imshow de la bibliothèque matplotlib.pyplot) , le petit axe de l'ellipse du cylindre est indiqué en bleu, fait 653 pixels et correspond à 2cm.

Les lignes en rouge mettent en évidence la ligne de pente et l'horizontale.

Limage=5120
fps=41
petitaxe_pix=653
petitaxe_m=0.02

• En effectuant des lectures simplement à l'oeil sur la figure précédente, estimez angle_pente l'angle de la pente en degrés. On pourra utiliser la fonction np.arccos ou np.arcsin ou np.arctan

angle_pente=None
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

La figure ci-dessous montre une série de 10 images accolées, où le temps va de gauche à droite, ligne après ligne. L'étudiant a sélectionné ici seulement une image sur deux par rapport au groupe entier d'images produit par la caméra.

• A quel temps en seconde a été prise la dernière image? On le mettra dans la variable tfinal.
• Construire Tvec le tableau numpy des temps associés à chaque image. On utilisera obligatoirement soit np.arange soit np.linspace.

tfinal=None
Tvec=None

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

A partir de cette image unique rassemblant les 10 images, l'étudiant a relevé les coordonnées en pixel du point marqué en rouge avec une croix sur chaque image en fonction du temps et créé les tableaux suivants:

xpixel= np.array([ 2329.7, 7553. , 12862. , 18282. , 23682. , 3331. , 8541. ,13793. , 19295. , 24977. ])

ypixel= np.array([2978.5, 3011. , 3078. , 3271. , 3557. , 8770. , 8788. , 8754. , 8529. , 8400. ])

• En effectuant une ou plusieurs boucles for et en utilisant l'extraction d'éléments d'un tableau numpy à l'aide d'indice, créer le tableau xreel de l'abscisse du point marqué par une croix en mètre. On prendra aussi l'abscisse du point marqué de l'image 0 comme origine des abscisses.

Attention: Tout tableau donné avec des valeurs brutes directement saisies à la main sans boucle ne donnera pas de point à cette question (mais vous permet de continuer la suite des questions).

xpixel= np.array([ 2329.7,  7553. , 12862. , 18282. , 23682. ,  3331. ,  8541. ,13793. , 19295. , 24977. ])
ypixel= np.array([2978.5, 3011. , 3078. , 3271. , 3557. , 8770. , 8788. , 8754. , 8529. , 8400. ])

xreel=None

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

• Tracer alors l'évolution de l'abscisse du point marqué par une croix en mètre en fonction du temps. On mettra les labels et un titre à la figure.

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

• Créer de même le tableau yreel donnant l'évolution de l'ordonnée du point marqué par une croix, en mètre. On prendra aussi l'ordonnée du point marqué de l'image 0 comme origine des ordonnées. En toute dernière étape, le signe du tableau des ordonnées sera changé en négatif pour la cohérence avec le cylindre qui descend la pente (rappel: avec imshow en python, le zéro des y est en haut comme illustré sur la toute première figure).

yreel=None
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

• Tracer alors sur une même figure l'évolution de l'abscisse du point marqué en mètre en fonction du temps (à tracer en bleu) et celle de l'ordonnée du point marqué en mètre en fonction du temps (à tracer en vert). On mettra une légende, les labels et un titre à la figure.

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

• Tracer finalement la trajectoire du point marqué par une croix en fonction du temps. On utilisera plt.axis("equal") pour avoir la même échelle en abscisse et ordonnée. On mettra les labels et un titre à la figure. Vous devriez obtenir la figure ci-dessous: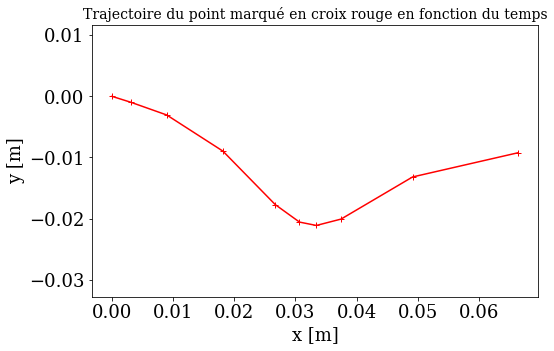

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

• Comment s'appelle ce type de trajectoire en mécanique? (écrire la phrase-réponse dans la cellule suivante en markdown )

Réponse:

YOUR ANSWER HERE

Partie III sur 10 pts

Le lâcher d'un ballon de basket a été effectué sur une planète inconnue. On souhaite retrouver la valeur de la constante gravitationnelle $g$ de cette planète.

La distance $d(t)$ entre la position initiale et la position à un instant t donné d'un coprs chutant sans frottement dans un champ de pesanteur suit la loi théorique : $ d_{theo}(t) = \frac{1}{2} \ g \ t^2$ où g est en $m/s^2$, t en secondes et d en mètres.

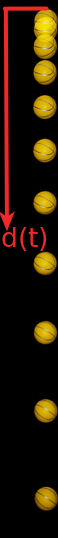
La photo ci-dessus met sur une seule image 11 instants différents d'un film.

La mesure de d est prise à partir de la position haute du ballon (sommet du ballon).

Lecture de l'image et taille pixel :

Le ballon de basket a un diamètre de 23.8cm.

• A l'aide des fonctions imread de la bibliothèque cv2 et imshow de la bibliothèque matplotlib.pyplot, lire et afficher l'image "Chute_libre.png"
• A l'aide du curseur en mode interactif, estimez la taille en pixel du ballon et en déduire le facteur de conversion d'un pixel en mètre que l'on stockera dans la variable taille_pix.

%matplotlib widget

taille_pix = None

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Relevé des positions de la partie haute du ballon et conversion en mètres :

• Relevez dans un tableau numpy dbr, les 11 positions en pixel de la position haute du ballon (sommet du ballon).
• Créez à l'aide de taille_pix et du tableau dbr, un tableau d qui contient ces positions en mètres. Le tableau d doit être tel que la première distance correspondant à t=0 est nulle.

dbr = None 
d = None
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Création d'un vecteur temps

Sachant que les 11 images sont séparées dans le temps par $dt = 0.25$ secondes. Créez un tableau numpy $t$ contenant le temps en secondes pour chaque position du ballon.

dt = None 
t  = None
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Tracé de la position en fonction du temps et estimation grossière de g

• Tracez la courbe $d(t)$ en couleur bleu avec des symboles '+'.
• Créez un tableau numpy gtab de 10 valeurs allant de 1. à 10. inclus.
• Superposez sur la courbe précédente, les 10 courbes théoriques pour les valeurs de gtab. Mettre un titre et des axes à la figure.
• Écrire dans une phrase réponse (précédée d'un #) un encadrement par deux valeurs entières la valeur de $g$ que vous déduisez du graphe précédent

%matplotlib inline
gtab = None 
# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Calcul de l'erreur et estimation fine de g

• Créez un tableau numpy gtabfin de 50 valeurs entre les deux valeurs entières trouvées à la question précédente
• Calculez l'erreur entre la courbe expérimentale et les courbes théoriques, au sens des moindres carrés pour les 50 valeurs de gtabfin, Stockez ces 50 valeurs dans un tableau Etab:

On rappelle que l'erreur au sens des moindres carrés est définie par : $$ E= \sqrt{ \sum_{i=1}^{11} (dtheo_i - d_i)^2 }$$.

• Tracez l'erreur en fonction de gtabfin
• A l'aide d'instruction python, cherchez g_expe : la valeur de $g$ pour laquelle l'erreur est minimum et l'afficher.

%matplotlib inline
g_expe = None

# YOUR CODE HERE
raise NotImplementedError()

# ne rien écrire dans cette cellule

Fin de l'examen

A la fin de l'examen, enregistrer votre travail (bouton à gauche), puis revenir à la fenêtre Nbgrader/Assignement list pour soumettre votre travail !